Playing With Mathematical Theories Together

The first graders have been exploring these questions:

How big is a number?

How do numbers work together to make new numbers?

These big, overarching questions provide the doorways into the mathematical landscape for children to theorize and investigate concepts such as addition, subtraction, skip counting, unitizing, and place value.

As teacher-researchers that believe in the social construction of knowledge and understanding, we are trying to stay focused on the children’s thinking and their jointly constructed meaning of the world, rather than on our own preconceived ideas about “the right answer.” We work to validate their attempts and to understand their sense-making in each moment. This supports meaning-making, but also the children’s growing confidence in the culture we are trying to create – one of sharing ideas and theories that are honored and valued for the understanding they uncover for each of us.

By inviting children to make their own meaning through playing with ideas, dialogue, and materials, children wrestle with theories, building deeper understanding and ownership.

“We construct not only the knowledge but also an awareness of how this construction takes place: exchange, dialog, divergence, negotiation, and also the pleasure of thinking and working together which is the real pleasure of friendship.” 

–Linda Pound and Trisha Lee

How are these children constructing their own understanding how numbers work? 

Of big ideas such as place value?

What follows below is a window into their mathematical thinking.

While sitting in a circle around a number line, IM shared her noticing with her math group about how zero might not be a big number but is a big deal because it is part of so many numbers.  She pointed out that the number line looks like it starts with the number ten, because the zero and the one are next to each other. This seemed to make several students uncomfortable and they responded that it could not be a ten.

ZB: It starts by the zero and then it keeps going on, you know? 0,1,2,3,4…

IM: I am saying zero upside down looks like ten. 

WK: (pointing to the number ten) This is a ten because why would a ten be at the start of a number line?

KNJ: Like if you are on Fiona’s side it looks like a ten but if you are on me and E’s side it looks like a zero and a one. 

Teacher: Hmmm . . . Does how you look at something change what you think?

Several Students: Yes. 

Teacher: Do you see what she is seeing with the one and the zero side by side from her perspective?

ZB: Yeah.

KJ: (Pointing to the number line) 0,1. . .0,1. . . .0,1 . . . 

SK: I notice they are always side by side.  Because look 0,1. . .0,1. . .0,1

PY: Why are they always side by side?

Instead of discounting IM’s idea, this group of children were supported in their attempt to understand her perspective, gather more information, and compare it to their own understanding. In other words, we were playing with ideas. Playing with an idea is important because it is not until we take the risk to play and wrestle with something that we start understand it.

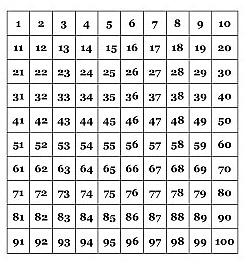
Afterward, we looked at a hundreds chart together.  As IM looked closely at the hundreds chart, she exclaimed, “I get it! I get it!  Look five and four go side by side too!”  Other students joined in her excitement and the class started to play together by looking at the patterns of numbers that live inside a hundreds chart.

EW: There is a five and a one (51), and a five and a two (52), and a five and a three (53), and a five and a four (54), and five and a five (55), and five and a six (56). . .

Teacher: It goes 1, 2, 3, 4, 5, 6, 7, 8, 9 . . . does it do it with every row?

Several Students: Yeah

EW: It does it with every singe number!

Teacher: Prove it. Does it do it with the nine’s?  What about the nine’s? (Referring to the 90’s row)

We count together on the 90’s row: 1, 2, 3, 4, 5, 6, 7, 8, 9

IM: It does it with the zero’s too. (Pointing to the tens column, 10, 20, 30, 40, 50,  . . .)

ZB: I have a problem. On the bottom there are two zero’s not one. (Referring to the number 100)

KV: If you take away the nine on here (90) then it would just be zero there.  And there are all zeros on this side and all the numbers are different. Maybe, they all have ten?

After the children left, I reflected on the meaning I saw being uncovered within the first grade group. I heard both articulated questions and unspoken wonderings. I saw a whole group of children involved and the energy was palpable and contagious. I thought, what if I hadn’t supported IM in her theory and simply discredited her noticing?

“When the teacher holds all the power of decision making, children become mentally passive because they are prevented from taking a stand, exchanging points of view….”

-Constance Kamii

I found myself wondering, maybe IM is right. Maybe zero is a big deal? Maybe there is a ten. . .  just not where we started looking for it. Or maybe it is there but it’s implied and we’re not supposed to see it. It was through IM taking a risk, sharing her wondering, and us being open to play in dialogue with her theory that we were lead to even bigger wonderings: the number’s position and what those numbers mean for us, the idea and system of place value, and the value of zero in our number system.

“Maybe, they all have ten?”- KV