Math Congress: Space for everyone to get on and off the subway

Math Congress is a structure that we use often at Opal School in which children are invited to communicate their thinking, their strategies, their solutions, “aha” moments, and proofs to their mathematical community.

As teachers, even with the clearest of intentions, Math Congress requires us to embrace uncertainty as we are never completely sure what questions will emerge, what ideas will be sparked, and where children may lead.

At a Math Congress not too long ago, students discussed their thinking and strategies for solving a problem that required imagining themselves on a subway train.

When the train pulls in the station there are 17 people on it.  The doors open and there is a flurry of activity.  When the train leaves the station there are 15 people on it.  How many people could have gotten on and how many people could have gotten off if you stayed on the train.  

Here’s some of the work behind what they shared:

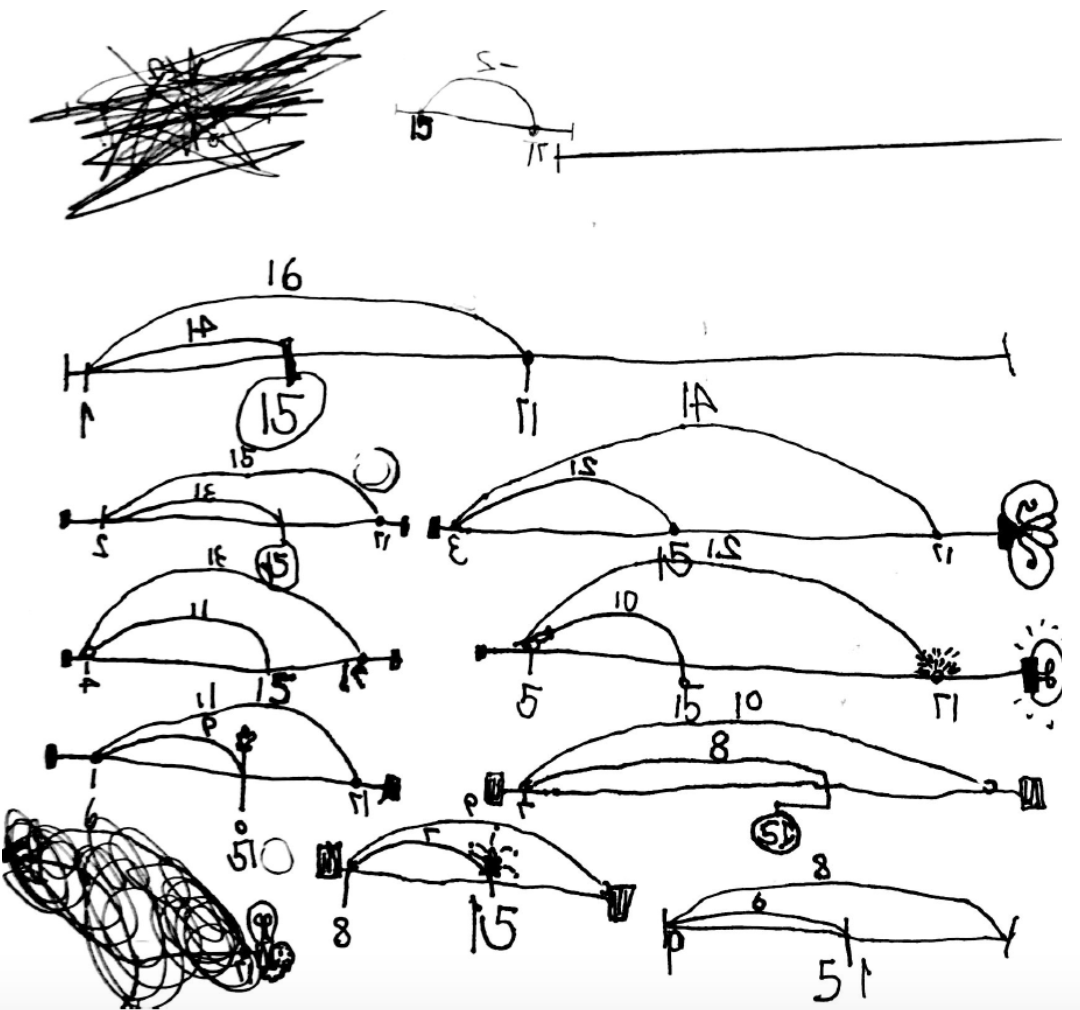
Before solving this problem, students solved a variety of subway problems in which there were more passengers on the train when it left the station than when the train arrived.  This new subway problem challenged students to rethink their strategies from the previous problems.  I imagine the content of the dialogue below may feel confusing without the whole context, but I invite you to focus more on the language of meaning-making as students try to understand each others’ thinking and revise their own in the process.   

As partners shared their work, we heard comments like:  

M:  I just started to get it more.  I realized the same thing, it did start with a lower number.

K:  17 people could get on if 1 got off.  Nevermind.  I just found some ways to add first.  My strategy is just swapped.

Z:  You just used that 17, just the other way around.  

K:  I think this is different because we land on different numbers.

I:  Well, I think we’re supposed to stay in a boundary and try to get 17.  

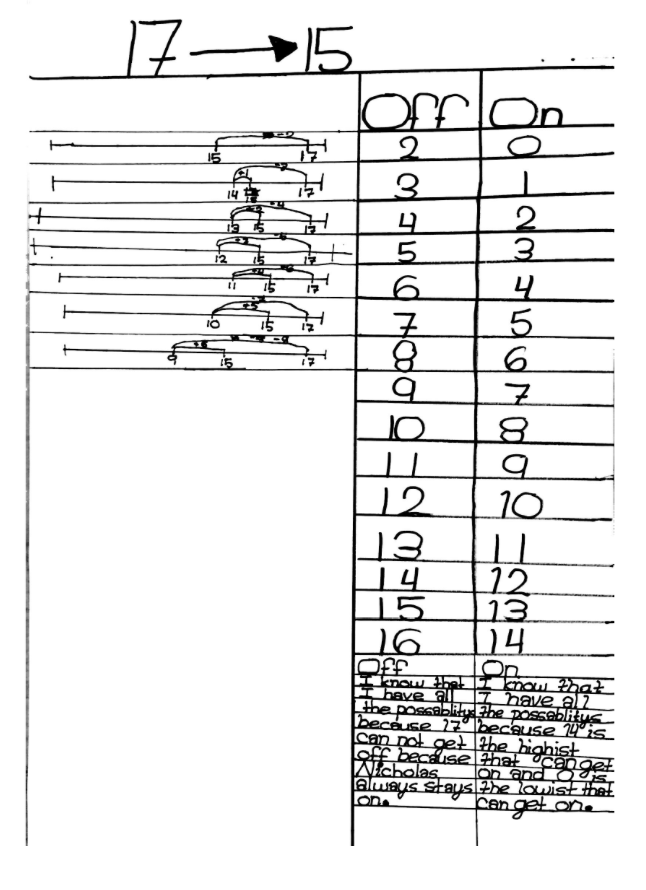
E:  Instead of doing that chart you did, we were writing down.  We had stuff here (pointing to a series of open number lines on a poster).  Does that help convince you we have all of the possibilities?

L:  It doesn’t always convince me for all of the possibilities.

P:  It helped convince me by a little bit.  

To me, these kinds of comments reveal children’s desire for meaning-making and their pursuit of understanding as they try to make sense of their own work in relationship to others’.  

And then, at the very end of Congress, after almost 45 minutes of intense sitting and dialogue, as the other classes began to pour onto the playground for recess, a final child raised her hand.

W:  I have a question. You’re saying 10 (people) couldn’t get off?  Did we already say this and it just didn’t make sense to me yet?  Where is the other boundary?  How many people can get on?

This question was powerful in that W so clearly articulated the possibility that her question had been answered earlier but if it had indeed, she simply wasn’t yet ready to understand it.  It took the journey of Math Congress for her to construct her own understanding, to be ready to ask her question, to connect to the work being shared.  This experience serves as reminder to me to create time and space to honor each individual’s process because sometimes we just aren’t ready to hear “it” yet.