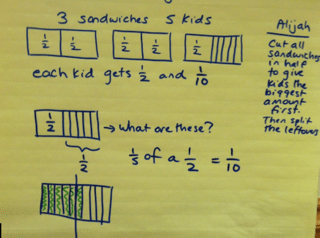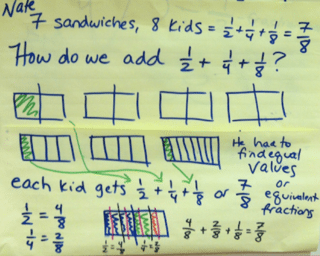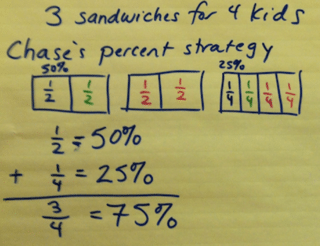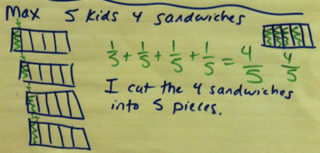Early Fraction Math Work: Math Congress

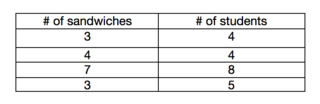
To launch our work with fractions, students were told a story about another class of fourth graders who were going on a small group field trips around New York City. They were sent with submarine sandwiches for lunch. Because the sandwiches were so big, they did not bring a whole sandwich for each child. Below you’ll see the group sizes and number of sandwiches.

We asked our fourth graders the following questions:

Was this fair?

How much did each student get, if the sandwiches were divided evenly?

After an initial discussion in which students used logic and proportional reasoning, students were quick to see that some groups definitely got more than others. Then, they set out to find out exactly how much the students on the field trip got.

After grappling with the problems for a while, developing strategies, and refining work, we came together for a congress. In a math congress, the class gathers to present and discuss strategies. Not everyone necessarily presents, but everyone is a part of the discussion. The students who present are learning as they share: As they think about how to communicate their understanding and anticipate and respond to classmates’ questions, their understanding deepens. Students who don’t formally share their work partake in the conversation with questions, comments, and connections.

Alijah started our congress. She explained that she used a strategy of cutting all the sandwiches in half so she could give everyone at least a half. Then, she divided what was left between the kids evenly.

When Alijah shared her thinking for 3 sandwiches and 5 kids, a question came up. When you split 1/2 into 5 pieces, what are they? Are they fifths or tenths? Through discussion and models,
the class came to see that they could not be called fifths because it was the pieces were not fifths of the whole sandwich, they were only fifths of half of the sandwich, or, in other words, tenths.

We looked at another problem with Alijah’s strategy: 4 kids and 3 sandwiches. It was pretty easy to see that we could give each kid 1/2 and 1/4. Lucius said, “That’s 3/4. I just know that.”

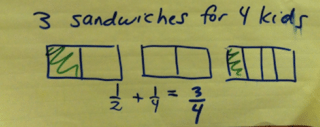
Then, Nate shared his work. He had figured out how to go from leaving your answer as 1/2 + 1/4 or 1/2 + 1/10. This was helpful for situations where you might not “just know it.”  Nate explained that if he thought about 1/2 + 1/4 + 1/8, he did know how to add them. But, if he thought about 1/2 as 4/8 and 1/4 as 2/8, then he could add 4/8 + 2/8 + 1/8 to get 7/8.

Liam and Roan explained Nate’s thinking, articulating that Nate had found equal values for the fractions he had. This gave us the opportunity to introduce the term equivalent fractions, which were what Liam and Roan were talking about, without yet knowing what they were called.

Chase offered a connection to Nate’s work with equivalency. She said that another way to think about the fractions was as percents. Chase said, “I know that ½ is the same as 50% and ¼ is the same as 25%, so I can just add the percents. That’s 75% and I know that is the same as ¾.”

Roan shared next. He explained that he took the amount of sandwiches and divided each sandwich into the number of kids. Then, he would try giving random amounts of pieces to each kid until he found and amount that would come out evenly.

Bridger spoke up, with some encouragement. He said, “That starts like my strategy, but then I did something different. Instead of trying random numbers, I divided the total number of pieces by the number of kids and that told me how many pieces they got.” Bridger saw a connection between his work and Roan’s and extended it to help Roan see a more efficient way to think about the problems.

Max had a different idea that many students went on to try. He started like Roan and Bridger by dividing all the sandwiches into the number of kids on the group. Then, he gave one piece of each sandwich to each kid. Then, he added the fractional pieces to find how much they each got.

Calvin and Thomas shared a finding they had discovered. They noticed a relationship between the numbers and the amounts the students got.

Calvin and Thomas noticed that the numbers in the problem always appeared in the answer. Calvin explained that the sandwiches were what you were splitting and that number was always on top. The kids were what you were splitting that number by and that was on the bottom.

This helped us see that the fraction bar between numbers really means “divided by.” 1 cookie divided by 2 people = ½. Nate made a connection to the bar in the division sign: ¸   “It’s like the numbers replace the dots – look how close they look!”

Now that the students had more understanding of what the numbers on top of and below the fraction bar meant, we introduced the terms numerator and denominator.

Then, Chloe wrapped up the congress by sharing her journey of thought through the investigation. She said, “First I started with the strategy of guessing random numbers to get to the number of sandwiches. It was hard. I did that for two problems and then I changed my strategy. I did something like Alijah’s strategy for the next one. And that was easier. Then, for the last one, I had trouble but Katharine helped me with a strategy and model, which was like Max’s but kind of the opposite. I drew pictures and took pieces away to give to each kid and what was left showed the answer. At the end I looked over my thinking and noticed the same thing as Calvin and Thomas. I noticed a lot of things after I did them that would have helped if I had known them earlier, but I had to start somewhere to be able to figure that out.”

In this investigation, which began with the story and ended with the congress, students grappled with key concepts for fractions. The story helped them come up with models (drawing sandwiches) which helped them come up with the strategies described above. They explored the connection between fractions and division, they began thinking about equivalent fractions, and they considered the idea that fractions are relations – the size or amount of the whole matters. They also encountered new vocabulary – equivalent fractions, numerator, denominator, fraction bar, and more. In their work and in the congress, they tried to articulate and justify their thinking. And this is just the beginning of our unit on fractions!